6. Operaciones con números complejos
Matlab incluye varias funciones que se usan principalmente con números complejos. Los números complejos consisten en dos partes: una parte real y un componente imaginario. Por ejemplo,
8 + 6i
es un número complejo. El componente real es 8 y el componente imaginario es 6. Los números complejos se pueden ingresar en Matlab de dos formas: como un problema de suma, como
A = 8 + 6i o A = 8 + 6*i
Con frecuencia, los números complejos se consideran como la descripción de una posición en el plano x-y. La parte real del número corresponde al valor x, y el componente imaginario corresponde al valor y, como se muestra en la Ilustración 6.1 (negro). Otra forma de pensar acerca de este punto es describirlo con coordenadas polares; esto es: con un radio y un ángulo (azul en la ilustración 42).

Anteriormente se revisó la función abs(),esta se puede utilizar con un número complejo para obtener el radio mediante el teorema de Pitágoras:
abs(A)
ans = 10
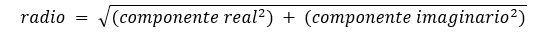
Puesto que, en este ejemplo, el componente real es 8 y el componente imaginario es 6,
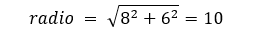
En la tabla 14 se resumen las funciones usadas con numero complejos.
Tabla 14. Funciones para números complejos.
| Función. | Descripción. | Ejemplo. |
| abs(x) | Calcula el valor absoluto de un numero complejo mediante el teorema de Pitágoras. Esto es equivalente al radio si el numero complejo se representa en coordenadas polares. Por ejemplo, si x = 3 + 4i, el valor absoluto es . | x = 3+4i; abs(x) ans = 5 |
| angle(x) | Calcula el ángulo desde la horizontal, en radianes, cuando un número complejo se representa en coordenadas polares. | x = 3+4i; angle(x) ans = 0,9273 |
| complex(x,y) | Genera un número complejo con un componente real x y un componente imaginario y. | x = 3; y = 4; complex(x,y) ans = 3.0000 + 4.0000i |
| real(x) | Extrae el componente real de un número complejo. | x = 3+4i; real(x) ans = 3 |
| imag(x) | Extrae el componente imaginario de un número complejo. | x = 3+4i; imag(x) ans = 4 |
| isreal(x) | Determina si los valores en un arreglo son reales. Si lo son, la función regresa 1; si son complejos, regresa 0. | x = 3+4i isreal(x) ans = 0 |
| conj(x) | Genera la conjugada compleja de un número complejo. | x = 3+4i conj(x) ans = 3.0000 – 4.0000i |
Ejercicio 6.1. Cree los siguientes números complejos (código en lustración 43, solución en ilustración 44).
a. A = 1 + i
b. B = 2 – 3i
c. C = 8 + 2i


Ejercicio 6.2. Cree un vector D de números complejos cuyos componentes reales son 2, 4 y 6 y cuyos componentes imaginarios son 23, 8 y 216 (código en lustración 45, solución en ilustración 46).


Ejercicio 6.3. Encuentre la magnitud (valor absoluto) de cada uno de los vectores que creó en los problemas 1 y 2 (código en lustración 47, solución en ilustración 48).


Ejercicio 6.4. Encuentre el ángulo desde la horizontal de cada uno de los números complejos que creó en los problemas 1 y 2 (código en lustración 49, solución en ilustración 50).


Ejercicio 6.5. Encuentre la conjugada compleja del vector D (código en lustración 51, solución en ilustración 52).


