7. Matrices y vectores
7.1. Funciones de análisis de datos.
Analizar datos estadísticos en MATLAB es particularmente sencillo, en parte porque todos los conjuntos de datos se pueden representar mediante una sola matriz y en parte debido a la gran cantidad de funciones internas de análisis de datos.
7.2. Máximo y mínimo.
La tabla 15 menciona las funciones que encuentran el mínimo y el máximo en un conjunto de datos y el elemento en el que ocurren dichos valores.
Tabla 15. Funciones para encontrar los máximos y mínimos en una matriz.
| Función. | Descripción. | Ejemplo. |
| max(x) | Encuentra el valor mas grande en un vector x. Por ejemplo, si x = [2 8 6], el valor máximo es 8. Crea un vector fila que contiene el elemento máximo de cada columna de una matriz x. Por ejemplo, si  , entonces el valor máximo en la columna 1 es 4, el valor máximo en la columna 2 es 8 y el valor máximo en la columna 3 es 6. | x = [2 8 6]; max(x) ans = 8 x = [2, 8, 6; 4, 5, 1]; max(x) ans = 4 8 6 |
| [a,b]=max(x) | Encuentra tanto el valor más grande en un vector x y su ubicación en el vector x. Para x = [2 8 6], el valor máximo se llama a y se encuentra que es 8. La ubicación del valor máximo es el elemento 2 y se llama b. Crea un vector fila que contiene el elemento máximo de cada columna de una matriz x y regresa un vector fila con la ubicación del máximo en cada columna de la matriz x. Por ejemplo, si , entonces el valor máximo en la columna 1 es 4, el valor máximo en la columna 2 es 8 y el valor máximo en la columna 3 es 6. Estos máximos ocurren en la fila 2, fila 1 y fila1, respectivamente. | x = [2 8 6]; [a,b]=max(x) a = 8 b = 2 x = [2, 8, 6; 4, 5, 1]; [a,b]=max(x) a = 4 8 6 2 1 2 |
| max(x,y) | Crea una matriz del mismo tamaño que x y y (tanto x como y deben tener el mismo número de filas y columnas). Cada elemento en la matriz resultante contiene el valor máximo de las posiciones correspondientes en x y y. Por ejemplo, si y 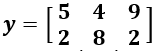 , entonces la matriz resultante será así  . | x = [2 8 6; 4 5 1] y = [5 4 9: 2 8 2] max(x,y) ans = 5 8 9 4 8 2 |
| min(x) | Encuentra el valor más pequeño en un vector x. Por ejemplo, si x= [2 8 6], el valor mínimo es 2. Creo un vector fila que contiene el elemento mínimo de cada columna de una matriz x. Por ejemplo, si ,entonces el valor mínimo en la columna 1 es 2, el valor mínimo en la columna 2 es 5 y el valor mínimo en la columna 3 es 1. | x = [2 8 6]; min(x) ans = 2 x = [2, 8, 6; 4, 5, 1]; min(x) ans = 2 5 1 |
| [a,b]=min(x) | Encuentra tanto el valor más pequeño en un vector x y su ubicación en el vector x. Para x = [2 8 6], el valor mínimo se llama a y se encuentra que es 2. La ubicación del valor mínimo es el elemento 1 y se llama b. Crea un vector fila que contiene el elemento mínimo de cada columna de una matriz x y regresa un vector fila con la ubicación del mínimo en cada columna de la matriz x. Por ejemplo, si , entonces el valor mínimo en la columna 1 es 2, el valor mínimo en la columna 2 es 5 y el valor mínimo en la columna 3 es 1. Estos mínimos ocurren en la fila 1, fila 2 y fila2, respectivamente. | x = [2 8 6]; [a,b] = min(x) a = 2 b = 1 x = [2, 8, 6; 4, 5, 1]; [a,b]=min(x) a = 2 5 1 1 2 1 |
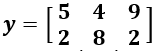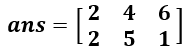| min(x,y) | Crea una matriz del mismo tamaño que x y y (tanto x como y deben tener el mismo número de filas y columnas). Cada elemento en la matriz resultante contiene el valor mínimo de las posiciones correspondientes en x y y. Por ejemplo, si y , entonces la matriz resultante será si  . | x = [2 8 6; 4 5 1] y = [5 4 9; 2 8 2] min(x,y) ans= 2 4 6 2 5 1 |
7.3. Media y mediana.
Existen muchas formas de encontrar el valor “promedio” en un conjunto de datos. En estadística, la media de un grupo de valores probablemente es lo que la mayoría llamaría el promedio. La media es la suma de todos los valores, divididos por el número total de valores. Otro tipo de promedio es la mediana, o el valor medio. Existe un número igual de valores tanto más grandes como más pequeños que la mediana. Matlab proporciona funciones para encontrar tanto la media como la mediana, como se muestra en la tabla 16.
Tabla 16. Funciones para encontrar la media y mediana en una matriz.
| Función. | Descripción. | Ejemplo. |
| mean(x) | Calcula el valor medio (o valor promedio) de un vector x. Por ejemplo, si x = [3 5 7], el valor medio es 5. Regresa un vector fila que contiene el valor medio de cada columna de una matriz x. Por ejemplo, si 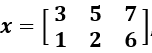 , entonces el valor medio de la columna 1 es 2, el valor medio de la columna 2 es 3.5 y el valor medio de la columna 3 es 6.5. | x = [3 5 7]; mean(x) ans = 5.0000 x = [3 5 7;1 2 6]; mean(x) ans = 1.5 4.5 4.5 |
| median(x) | Encuentra la mediana de los elementos de un vector x. Por ejemplo, si x = [3 5 7], el valor mediana es 3. Por ejemplo, s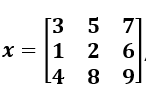 , entonces el valor mediana de la columna 1 es 3, el valor mediana de la columna 2 es 5 y el valor mediana de la columna 3 es 8. | x = [3 5 7]; median(x) ans = 5 x = [3 5 7;1 2 6;4 8 9]; median(x) ans = 3 5 8 |
7.4. Sumas y productos.
Con frecuencia es útil sumar todos los elementos en una matriz o multiplicar todos los elementos juntos. Matlab proporciona algunas funciones para calcular tanto sumas como productos, como se muestra en la tabla 17.
Tabla 17. Sumas y productos en Matlab.
| Función. | Descripción. | Ejemplo. |
| sum(x) | Suma los elementos en el vector x. Por ejemplo, si x = [2 6 1], la suma es 9. Calcula un vector fila que se contiene la suma de los elementos de cada columna de una matriz x. Por ejemplo, si 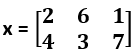 , Entonces la suma de la columna 1 es 6, la suma de la columna 2 es 9 y la suma de la columna 3 es 8. | x = [2 6 1]; sum(x) ans = 9 x = [2 6 1; 4 3 7] sum(x) ans = 6 9 8 |
| prod(x) | Calcula el producto de los elementos de un vector x. Por ejemplo, si x = [2 6 1], la suma es 12. Calcula un vector fila que se contiene el producto de los elementos de cada columna de una matriz x. Por ejemplo, si 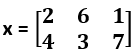, Entonces la suma de la columna 1 es 8, la suma de la columna 2 es 18 y la suma de la columna 3 es 7. | x = [2 6 1]; prod(x) ans = 12 x = [2 6 1; 4 3 7] prod(x) ans = 8 18 7 |
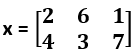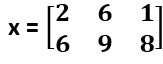| cumsum(x) | Calcula un vector del mismo tamaño que un vector x y contiene sumas acumuladas de los elementos del mismo. Por ejemplo, si x = [2 6 1], el vector resultante es x = [2 8 9]. Calcula una matriz que contiene la suma acumulada de los elementos en cada columna de una matriz x. Por ejemplo, si , la matriz resultante es  . | x = [2 6 1]; cumsum(x) ans = 2 8 9 x = [2 6 1; 4 3 7]; cumsum(x) ans = 2 6 1 6 9 8 |
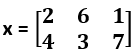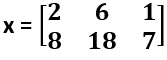| cumprod(x) | Calcula un vector del mismo tamaño que un vector x y contiene productos acumulados de los elementos del mismo. Por ejemplo, si x = [2 6 1], el vector resultante es x = [2 12 12]. Calcula una matriz que contiene el producto acumulado de los elementos en cada columna de una matriz x. Por ejemplo, si , la matriz resultante es  . | x = [2 6 1]; cumprod(x) ans = 2 12 12 x = [2 6 1; 4 3 7]; cumprod(x) ans = 2 6 1 8 18 7 |
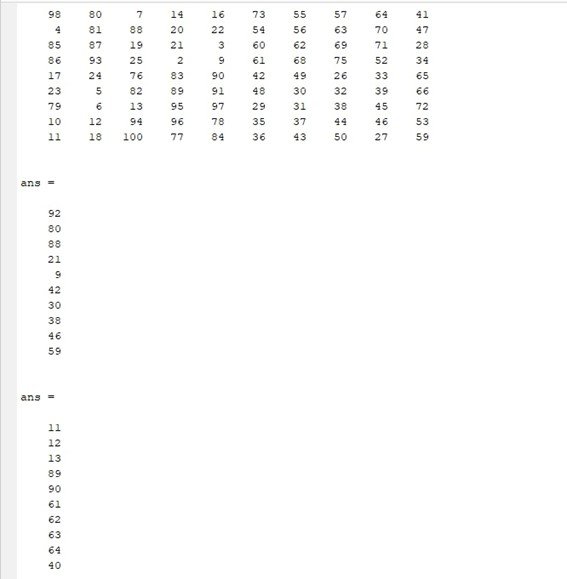
Considere la siguiente matriz:
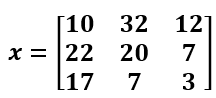
Ejercicio 7.4.1. ¿Cuál es el valor máximo en cada columna? (Código en lustración 53, solución en ilustración 54).
Ejercicio 7.4.2. ¿En cuál fila se presenta dicho máximo? (Código en lustración 55, solución en ilustración 56).
Ejercicio 7.4.3. ¿Cuál es el valor medio en cada columna? (Código en lustración 57, solución en ilustración 58).
Ejercicio 7.4.4. ¿Cuál es la mediana para cada columna? (Código en lustración 59, solución en ilustración 60).
Ejercicio 7.4.5. ¿Cuál es la suma en cada columna? (Código en lustración 61, solución en ilustración 62).
7.5. Ordenar datos y determinación del tamaño de matriz.
En la tabla 18 se mencionan las funciones para ordenar datos en una matriz y también para conocer sus dimensiones.
Tabla 18. Funciones para ordenar y determinar el tamaño de matriz.
| Función. | Descripción. | Ejemplo. |
| sort(x) | Ordena los elementos de un vector x en orden ascendente. Por ejemplo, si x = [1 8 3], el vector resultante es [1 3 8]. Ordena los elementos en cada columna de una matriz x en orden ascendiente. Por ejemplo, si 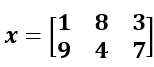 , la matriz resultante es . | x = [1 8 3]; sort(x) ans = 1 3 8 x = [1 8 3; 9 4 7]; sort(x) ans = 1 4 3 9 8 7 |
| sort(x,’descend’) | Orden los elementos en cada columna en orden descendente. | x = [1 8 3; 9 4 7]; sort(x,’descend’) ans = 9 8 7 1 4 3 |
| sortrows(x) | Ordena las filas en una matriz sobre la base de los valores en la primera columna y mantiene intacta cada fila. Por ejemplo, si 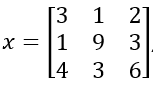 , Entonces usar el comando sortrows moverá la fila media hacia la posición superior. | x = [3 1 2; 1 9 3; 4 3 6]; sortrows(x) ans = 1 9 3 3 1 2 4 3 6 |
| sortrows(x,n) | Ordena las filas en una matriz sobre la base de los valores en la columna n. | sortrows(x) ans = 3 1 2 4 3 6 1 9 3 |
| size(x) | Determina el número de filas y columnas en la matriz x. | x = [3 1 2; 1 9 3; 4 3 6]; size(x) ans = 2 3 |
| [a,b] = size(x) | Determina el número de filas y columnas en la matriz x y asigna el número de filas a a y el número de columnas a b. | [a,b] = size(x) a = 2 b= 3 |
| length(x) | Determina la dimensión más grande de una matriz x. | x = [3 1 2; 1 9 3; 4 3 6]; length(x) x = 3 |
Considere la siguiente matriz:
Ejercicio 7.5.1. Use la función size para determinar el número de filas y columna en esta matriz (código en lustración 65, solución en ilustración 66).
Ejercicio 7.5.2. Use la función sort para ordenar cada columna en orden ascendente (código en lustración 67, solución en ilustración 68).
Ejercicio 7.5.3. Use la función sort para ordenar cada columna en orden descendente (código en lustración 69, solución en ilustración 70).
Ejercicio 7.5.4. Use la función sortrows para ordenar la matriz de modo que la primera columna esté en orden ascendente, pero cada fila todavía conserve sus datos originales (código en lustración 71, solución en ilustración 72).
7.6. Manipulación de Matrices.
En Matlab, una matriz se puede definir al escribir una lista de números encerrada entre corchetes. Los números se pueden separar mediante espacios o comas, a discreción del usuario. (Incluso puede combinar las dos técnicas en la misma definición de matriz.) Las nuevas filas se indican con punto y coma. Por ejemplo,
A = [3.5]
B = [1.5, 3.1]; o B = [1.5 3.1]
C = [-1, 0, 0; 1, 1, 0; 0, 0, 2].
También se puede definir una matriz al hacer una lista de cada fila en una línea separada, como en el siguiente conjunto de comandos MATLAB:
C = [-1, 0, 0;
1, 1, 0;
1, -1, 0;
0, 0, 2]
Incluso no necesita ingresar el punto y coma para indicar una nueva fila. MATLAB interpreta
C = [-1, 0, 0
1, 1, 0
1, -1, 0
0, 0, 2]
como una matriz de 4×3. También podría ingresar una matriz columna de esta forma:
A = 1
2
3
Si existen demasiados números en una fila como para encajar en una línea, puede continuar el enunciado en la línea siguiente, pero se requieren una coma y una elipsis (…) al final de la línea, lo que indica que la fila continúa. También puede usar la elipsis para continuar otros enunciados de asignación largos en MATLAB.
Para definir Z con 10 valores, se podría usar cualquiera de los siguientes enunciados:
Z = [10, 16, 20, 5, 3, 1, 17, 12, 16, 20]
Z = [10, 16, 20, 5, 3, 1, …
17, 12, 16, 20]
MATLAB también le permite definir una matriz en términos de otra matriz que ya se haya definido. Por ejemplo, los enunciados
B = [1.5 3.1]
S = [3.0, B]
regresa
S =
3.0 1.5 3.1
De manera similar,
T = [ 1, 2, 3; S]
regresa
T =
1 2 3
3 1.5 3.1
Se pueden cambiar los valores en una matriz, o incluir valores adicionales, con un número índice para especificar un elemento particular. Este proceso se llama indexación en un arreglo. Por tanto, el comando
S(2) = -1.0;
cambia el segundo valor en la matriz S de 1.5 a 21. Si escribe el nombre de matriz
S
en la ventana de comandos, entonces MATLAB regresa
S =
3.0 -1.0 3.1
También se puede extender una matriz al definir nuevos elementos. Si ejecuta el comando
S(4) = 5.5;
se extiende la matriz S a cuatro elementos en lugar de tres. Si se define el elemento
S(8) = 9.5;
la matriz S tendrá ocho valores, y los valores de S(5), S(6) y S(7) se establecerá a 0. En consecuencia,
S
regresa
S =
3.0 -1.0 3.1 5.5 0 0 0 9.5
El operador dos puntos es un operador muy poderoso para definir nuevas matrices y modificar las existentes. Primero, puede definir una matriz igualmente espaciada con el operador dos puntos. Por ejemplo,
H = 1:8
regresa
H =
1 2 3 4 5 6 7 8
El espaciamiento por defecto es 1. Sin embargo, cuando se usan los dos puntos para separar tres números, el valor medio se convierte en el espaciamiento. Por tanto,
Time = 0.0: 0.5: 2.0
regresa
time =
0 0.5000 1.0000 1.5000 2.0000
El operador dos puntos también se puede usar para extraer datos de las matrices, una característica que es muy útil en análisis de datos. Cuando en una matriz se usan dos puntos como referencia en lugar de un número índice específico, los dos puntos representan toda la fila o columna.
M = [1 2 3 4 5;
2 3 4 5 6;
3 4 5 6 7];
Se puede extraer la columna 1 de la matriz M con el comando
x = M(:, 1)
lo que regresa
x = 1
2
3
Esta sintaxis se puede leer como “todas las filas en la columna 1”. Puede extraer cualquiera de las columnas en una forma similar. Por ejemplo,
y = M(:,4)
regresa
y =
4
5
6
y se puede interpretar como “todas las filas en la columna 4”. De igual modo, para extraer una fila,
z = M(1,:)
regresa
z =
1 2 3 4 5
y se lee como “fila 1, todas las columnas”
No tiene que extraer toda una fila o toda una columna. El operador dos puntos también se puede usar para significar “desde fila _ hasta fila _” o “desde columna _ hasta columna _”. Para extraer las dos filas inferiores de la matriz M, escriba.
w = M(2:3,:)
que regresa
w =
2 3 4 5 6
3 4 5 6 7
y se lee “filas 2 a 3, todas las columnas”. De manera similar, para extraer sólo los cuatro números en la esquina inferior derecha de la matriz M,
w = M(2:3,4:5)
regresa
w =
5 6
6 7
y lee “filas 2 a 3 en las columnas 4 a 5”.
En MATLAB, es válido tener una matriz que esté vacía. Por ejemplo, los siguientes enunciados generarán cada uno una matriz vacía:
a = []
b = 4:-1:5;
Finalmente, usar el nombre de matriz con un solo dos puntos, como
M(:)
transforma la matriz en una larga columna.
M =
1
2
3
2
3
4
3
4
5
4
5
6
5
6
7
La matriz se formó al listar primero la columna 1, luego agregar la columna 2 al final, tomar la columna 3, etcétera. En realidad, la computadora no almacena arreglos bidimensionales en un patrón bidimensional. Más bien, “piensa” en una matriz como en una larga lista, tal como la matriz M a la izquierda: al usar un solo número índice o al usar la notación fila, columna. Para encontrar el valor en la fila 2, columna 3, use los siguientes comandos:
M
M =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
M(2,3)
ans =
4
De manera alternativa, puede usar un solo número índice. El valor en la fila 2, columna 3 de la matriz M es el elemento número 8. (Cuente la columna 1, luego la columna 2 y finalmente en la columna 3 hasta el elemento correcto.) El comando MATLAB asociado es
M(8)
ans = 4
Se puede usar la palabra “end” para identificar la fila o columna final en una matriz, incluso si no sabe qué tan grade es. Por ejemplo,
M(1,end)
regresa
M(1,end)
ans =
5
y
M(end,end)
regresa
ans =
7
como lo hace
M(end)
ans =
7
Cree variables MATLAB para representar las siguientes matrices y úselas en los ejercicios que siguen:
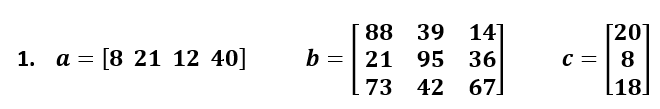
Ejercicio 7.6.1. Asigne a la variable x1 el valor en la segunda columna de la matriz a. En ocasiones, esto se representa en los libros de matemáticas como el elemento a1,2 y se podría expresar como x1 = a1,2 (código en lustración 73, solución en ilustración 74).
Ejercicio 7.6.2. Asigne a la variable x2 la tercera columna de la matriz b (código en lustración 75, solución en ilustración 76).
Ejercicio 7.6.3. Asigne a la variable x3 la tercera fila de la matriz b (código en lustración 77, solución en ilustración 78).
Ejercicio 7.6.4. Asigne a la variable x4 los valores en la matriz b a lo largo de la diagonal (es decir: elementos b1,1, b2,2 y b2,3). (Código en lustración 79, solución en ilustración 80).
Ejercicio 7.6.5. Asigne a la variable x5 los primeros tres valores en la matriz a como la primera fila y todos los valores en la matriz b como la segunda a la cuarta filas (código en lustración 81, solución en ilustración 82).
Ejercicio 7.6.6. Asigne a la variable x6 los valores en la matriz c como la primera columna, los valores en la matriz b como las columnas 2, 3 y 4, y los valores en la matriz a como la última fila (código en lustración 83, solución en ilustración 84).
Ejemplo Ejercicio 7.6.7. Asigne a la variable x7 el valor del elemento 8 en la matriz b (código en lustración 85, solución en ilustración 86).
Ejercicio 7.6.8. Convierta la matriz b en un vector columna llamado x8 (Código en lustración 87, solución en ilustración 88).
7.7. Matrices especiales.
Matlab contiene un grupo de funciones que generan matrices especiales; en la tabla 19 se presentan algunas de dichas funciones.
Tabla 19. Funciones para matrices especiales.
| Función. | Descripción. | Ejemplo. |
| zeros(m) | Crea una matriz m x m de ceros. | zeros(2) ans =  |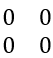
| zeros(m,n) | Crea una matriz m x n de caras. | zeros(2,3) ans =  |
| ones(m) | Crea una matriz m x m de unas. | ones(2) ans =  |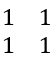
| ones(m,n) | Crea una matriz m x m de unos. | ones(2,3) ans =  |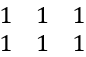
| diag(A) | Extrae la diagonal de una matriz bidimensional A. Para cualquier vector A, crea una matriz cuadrada con A como la diagonal. | De la matriz 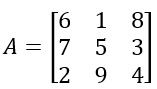 A = [6 1 8, 7 5 3, 2 9 4]; diag(A) ans = 6 5 4 A = [8 4 2]; diag(A) ans =  |
| fliplr(M) | Voltea una matriz en su imagen especular de derecha a izquierda. | De la matriz 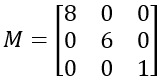 M = [8 0 0, 0 6 0, 0 0 1]; fliplr(M) ans =  |
| flipud(M) | Voltea una matriz verticalmente. | flipud(M) ans =  |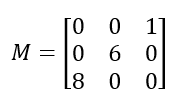
| magic(m) | Crea una matriz “mágica” m x m. Nota: una matriz “mágica” es aquella que todos los elementos en todas sus filas y columnas suman los mismo. | magic(3) ans =  |
Ejercicio 7.7.1. Cree una matriz 3 x 3 de ceros (código en lustración 89, solución en ilustración 90).
Ejercicio 7.7.2. Cree una matriz 3 x 3 de unos (código en lustración 91, solución en ilustración 92).
Ejercicio 7.7.3. Cree una matriz M de 3 x 4 en la que todos los elementos tengan un valor de pi (código en lustración 93, solución en ilustración 94).
Ejercicio 7.7.4. La función diag para crear una matriz cuya diagonal tenga valores de 1, 2, 3 (código en lustración 95, solución en ilustración 96).
Ejercicio 7.7.5. Cree una matriz mágica Z de 10×10 (código en lustración 97, solución en ilustración 98).
- Extraiga la diagonal de esta matriz.
- Extraiga la diagonal que corre de inferior izquierda a superior derecha de esta matriz.
